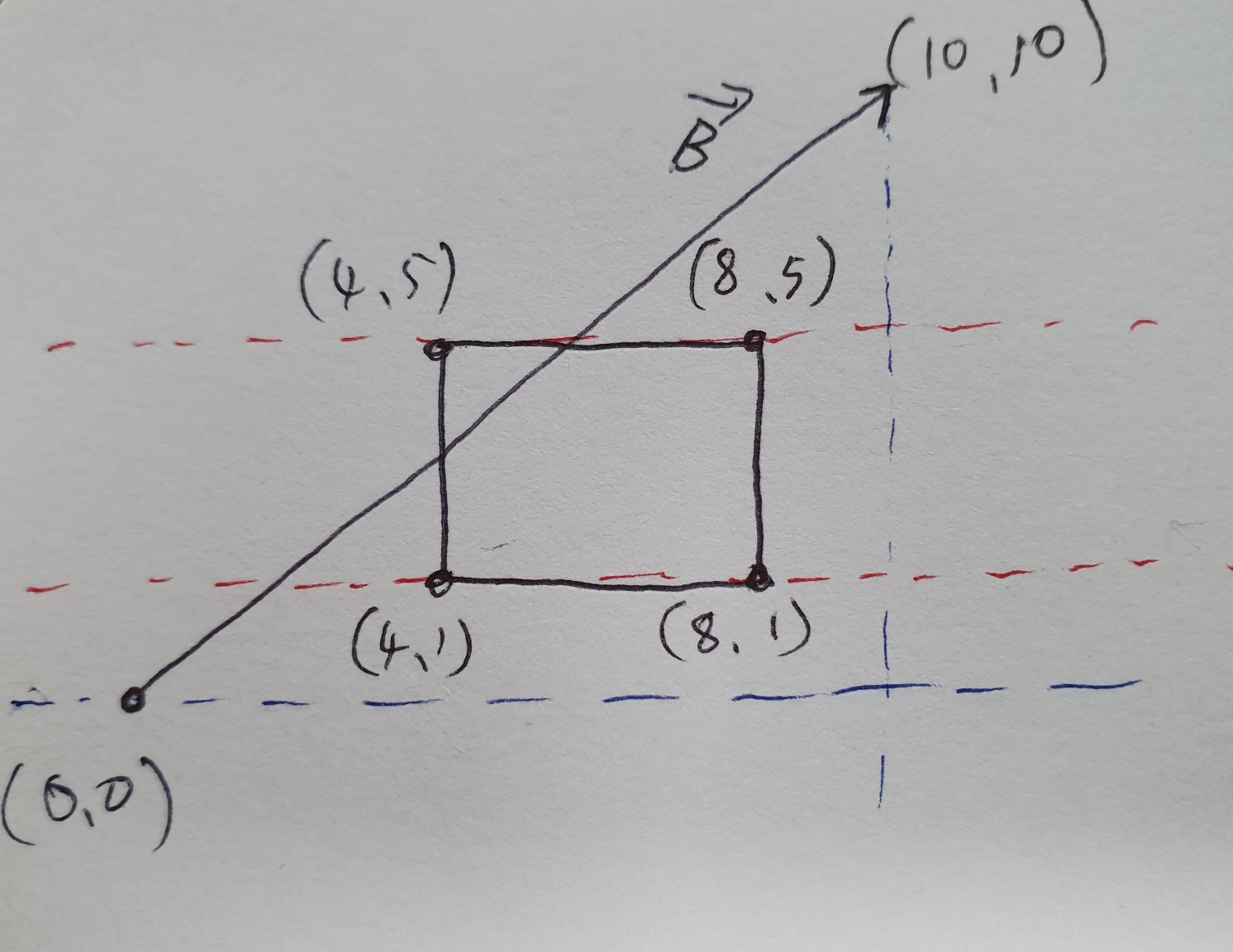


삼각형의 닮음 성질을 이용해 어떤 벡터와 x,y 축에 평행한 변을 가진 사각형의 collision check를 하는 방법이다.
3차원에서도 여기서 축 하나만 더 추가하면 같은 원리로 판정이 가능하다.
만약 사각형이 축에 평행하지 않다면 어떻게 해야 할까? 뒤에서 다루는 내용인 사각형의 각 좌표에 TRS Matrix를 곱해주어 사각형이 회전한 상태라고 가정해보자. 이 상태에서 어떤 벡터(직선)와의 충돌을 판정하려면 단순히 이 사각형을 다시 축에 평행하게 이동시키고, 이 벡터도 동일한 상대적 위치를 유지하도록 이동시켜주면 된다.

정리하면, 각 변이 축에 평행하지 않은 사각형과 어떤 벡터의 충돌을 판정하려면, 사각형의 꼭짓점들과 판정하려는 벡터에 TRS의 역행렬, 즉 S^-1 * R^-1 * T^-1을 곱해주어 x,y축을 기준으로 하는 좌표계로 이동시킨 뒤(=상대좌표계로 변환), 위에 서술된 AABB Intersection 알고리즘을 사용해주면 된다.
'mathematics > game mathematics' 카테고리의 다른 글
| [Mathematics] 7. Billboarding (0) | 2022.02.01 |
|---|---|
| [Mathematics] 6. 총알 소리 (Bullet whizzes) (0) | 2022.01.23 |
| [Mathematics] 4. Interpolation (0) | 2022.01.20 |
| [Mathematics] 3. 벡터의 외적 (0) | 2022.01.15 |
| [Mathematics] 2. Euler angle (0) | 2022.01.15 |
