Projection matrix(투영 행렬)은 아주 중요하고 아주 널리 다루어지지만 완벽하게 이해하기 까다로운 내용이다.
본 학습에서는 이를 최대한 완벽하게 이해할 수 있도록 다뤄보겠다.
본 학습에서 구현하고자 하는 기능은 화면 ratio 조절, fov 조절이다.
그리고 이 기능들을 추가하기 위한 더 나은 frustum을 사용한 projection 방법을 적용할 것이다.
(Frustum이 뭔지는 잠시 뒤에서 다루겠다)
그리고 이 Frustum을 사용한 projection 방법은 정점에 Projection matrix를 곱하는 과정을 통해 이루어지는데, 우리는 이 과정에 필요한 이 projection matrix를 구하는 과정을 살펴볼 것이다.

우리의 프레임워크에서는 현재로써는 focal plane(Frustum의 사각형 면)의 비율을 조정하는 기능이 아직 구현되지 않았고, 애초에 Frustum도 구현되어 있지 않다.
본격적으로 시작하기 전에, Vec4의 w에 대한 간략한 이해 및 우리가 지금 사용중인 Perspective projection에 대한 Recap이 권장된다. 19.Mat4, Vec4 및 4.perspective_projection을 참고하자.
해당 내용의 결론만을 이야기하면, 우리는 focal point(좌측 점/초점)와 focal plane(하늘색 면)에 의해 field of view를 형성했다.
그리고 focal point를 화면의 스크린에 맵핑해서 비치는 상이 화면 상에 렌더링되는 기법이 perspective projection이다.
즉 그림 상 보이는 두 긴 하늘색 선이 이루는 각이 우리의 field of view이다.
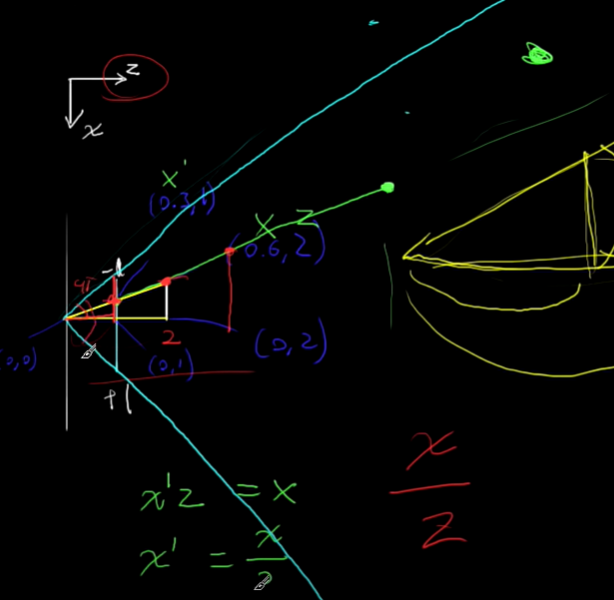
그리고 이 fov를 높이는 방법은 focal plane의 크기를 키우거나 혹은 focal plane과 focal point의 거리를 줄이거나 하는 방법이 있었다.
이 focal plane의 비율을 변경할 수 있는 기능 또한 구현해야 하는데, fov를 조정하는 기능 및 focal plane 비율을 조정하는 기능을 모두 구현해 보자.
(현재 파이프라인은 현재 1:1 ratio를 상수로 고정해두고 사용중이다.)
위 내용을 이해했다면, 이제 우리가 구현할 더 제대로 된 Projection Matrix에 대해 살펴보자.
우리는 Frustum과 NDC Space를 사용해 3차원 물체를 렌더링할 것이다.
자세히 살펴보자.

어떤 물체를 그릴 때 x,y축으로만 제한을 두는 게 아니라(시야각), z축으로도 제한을 두면(=일정 거리 사이의 물체만 렌더링하게 만들면) 위 사진처럼 사각뿔의 끝부분을 자른 듯한 입체도형 형태가 된다.
우리는 이를 Frustum이라고 한다.
Frustum의 가장 안쪽 면(연두색)이 Focal plane이다. (스크린과 맵핑되어있는 면)

화면 속에 보이는 저 물체들의 각 좌표들(정점들)에
1) Projection matrix를 곱한 이후
2) perspective division을 해주면(x/z 해줬던 과정이 perspective division) 저 Frustum 내부의 모든 공간이 우측의 직육면체 내부로 맵핑되게 된다.
이 직육면체 공간을 우리는 NDC Space라고 한다.
(이때 NDC Space는 화면의 ratio랑은 상관없이 항상 저 비율을 유지한다는 것에 주의하자. 또한 -1 ~ 1로 맵핑하는 x,y와 다르게 z는 0 ~ 1임에 유의하자.)
이를 구현하기에 앞서, 수학적 원리 (derivation)을 간략하게 살펴보자.
Frustum 정점이 NDC Space의 정점으로 맵핑되는 과정은 다음과 같이 두 단계로 나눠진다.
1) Frustum 내의 3d space에 위치한 Vec4 정점 v와 Projection matrix P를 곱해 NDC Space 내의 좌표로 나타내는 것 (+2번 perspective division을 준비하기 위해 Vec4의 w값 수정하기)
2) perspective division의 처리 (Vec4의 w(=z값)로 나누기)
이다. 이를 명심한 채로 계속 학습해 나가자.
우선 2번부터 다뤄보자.
perspective division은 결국 나눗셈이다. 때문에 Vec4에서 나눗셈을 간단하게 처리할 수 있게 하는 방법에 대해 살펴보자.
그리고 Vec4에서 나눗셈을 간단하게 처리할 수 있게 하는 방법을 알아보기 위해,
우선 homogeneous coordinates에 대해 알아보자.

우리는 이전 학습 내용에서 대부분의 Vec4의 w는 1이고, w를 0으로 만드는 것으로 벡터-행렬 곱에서 행렬의 가장 마지막 행을 무시해버릴 수 있음을 배웠다.

이 방법으로 우리는 normal 벡터들에 translation을 무시시킨채 Transform matrix를 곱해버릴 수 있었다.
즉 w의 값에 따라 행렬의 마지막 행이 주는 영향력이 결정됨을 알 수 있다.
그리고 이 w의 값이 1이 아닌 Vec4 정점을 우리는 3d space가 아닌,
projective space에 있는 정점,
혹은 homogeneous coordinates라고 부른다.
이제 왜 homogeneous coordinates라는 걸 방금 언급했는지, 이게 어떻게 Vec4의 나눗셈에 쓰이는지 알아보자.

homogeneous coordinate를 다시 normal space로 되돌리려면 w를 1로 만들면 되는데, w를 1로 만들려면 벡터 전체를 w로 나누면 된다. 이 과정을 우리는 Vec4의 "normalization"이라고 부른다.
Length를 1로 만든다는 개념의 Vec3의 normalization과 아주 헷갈리지만, 헷갈리지 않게 주의하자. (애초에 이전 포스트에서 벡터를 구현할 때 Vec4의 Length를 정의하지 않은 이유도 이 때문이기도 하다.)
만약 우리의 프레임워크 전체에서 Vec4를 "normalize"하도록 만든다면 우리의 파이프라인은 Vec4를 w로 나눌 것이고, 이렇게 파이프라인을 만든다면 우리는 w에 우리가 나눴으면 하는 값을 집어넣어 나눗셈을 보다 편리하게 처리할 수 있을 것이다. (ex. w에 z를 넣는 것으로 perspective division을 처리하는 등)
이러한 원리로 Vec4의 normalize를 이용해 perspective division을 하려면 normalization이 진행되기 전에 w값 = z이 되어야 할 필요가 있다. 우리는 이 과정 또한 projection matrix의 행렬곱 연산 내에 포함시킬 것이다.

그러기 위해서 위 사진처럼 행렬 (3,4)를 1로, (4,4)를 0으로 해놓으면 z는 남고 w(여기서 1)는 사라지게 되어 최종적으로 결과값 w는 z가 되게 만들 수 있다.
이렇게 2번 과정을 Projection matrix이 나타낼 수 있게 만들었다.
이제 Projection matrix의 나머지 부분들을 채워나가보자.

우리가 궁극적으로 projection matrix를 통해 얻으려는 것은 Frustum 내의 좌표들을 NDC Space로 맵핑하는 것이다. 즉 사진 속 Frustum의 윗쪽 빨간 부분이 NDC 윗쪽면과 맵핑되어야 한다.

사진의 하얀 부분에 주목해보자. Frustum을 위에서 내려다본 단면이라고 생각하면 이해가 빠르다. 우리는 Focal plane의 양끝점이 -1,+1이 되어야 함을 볼 수 있다. 마찬가지로 Frustum의 넓은면쪽 끝도 -1,+1이 되어야 한다.

그런데 Focal plane과 초점과의 거리가 변하거나, 혹은 Focal plane 자체의 크기가 변한다면 같은 정점이더라도 NDC Space 내에 맵핑되는 값이 변하게 된다.

이를 수식으로 나타내면 다음과 같다.
w는 Focal plane의 폭(width),
n은 Focal plane과 초점(Focal point)와의 거리일때
x', 즉 정점 x가 NDC에 맵핑되는 값 x'은 w/2에 반비례하고 n에 비례함을 알 수 있다.
y도 마찬가지의 원리로 생각해보면, 우리는 정점의 x,y가 NDC에 맵핑되도록 다음과 같은 행렬식을 유도해낼 수 있다.
(y의 경우 Focal plane의 높이(height)를 사용함에 유의)
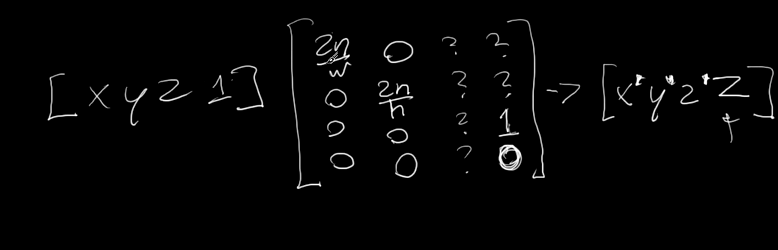

z의 경우, 우리는 Frustum의 가장 가까운 면이 z'=0이 되어야 하고, 가장 먼 면이 z'=1이 되어야 한다.

가까운 면은 그냥 z값 - n을 해주면 되어 어렵지 않다. (n은 앞서 말한것처럼 plane과 초점의 거리)
그래서 다음과 같이 행렬식을 변경해줄 수 있다.

먼 면의 경우, 일단 가까운 면과 먼 면의 거리를 구한다. (Frustum의 길이)
그리고 그 range의 정점들을 0~1 사이의 값들로 interpolate해줄 것이다.
때문에 방금 전 변경한 행렬식을 지워주고, 어떤 하나의 통일된 식으로 0~1의 범위에 맵핑할 수 있게 행렬식을 고쳐보자.

우리는 n(가까운면)에 있을 때 0이 나와야 하고, f(먼 면)에 있을 때 1이 나오게 고쳐야 한다.
여기서 우리는 두 식을 도출할 수 있다.
an + b = 0
af + b = f
af + b = 1이 아니냐고 반문할 수 있지만, 있지 말아야 할 게 우리는 Projection matrix를 곱한 이후 얻은 좌표에 Vec4 normalization을 처리해 w값(=z)로 나누어 perspective division을 처리해줄 것이라는 점이다.
이때 f(먼 면)의 경우 w에 들어있는 z값이 f일 것이기 때문에 f/f = 1이 되어 제대로 0~1로 맵핑되게 된다.
(간단히 말해, 아직 perspective division이 처리되기 전이기 때문에 곧장 1로 맵핑되면 안된다는 것이다)
어쨌든 이 두 식을 빼서 다음과 같이 a를 n과 f로 표현할 수 있다.

a를 대입해 b도 구할 수 있다.

이렇게 구한 a, b를 행렬에 추가하면, 드디어 완전한 projection matrix를 구할 수 있게 된다!


이 맵핑과정에서 한가지 주의해야 할 것은, 이 맵핑 과정이 linear 하지 않다는 점이다.
즉 n,f 정 중앙에 있는 점이 NDC에서 0과 1의 정중앙인 0.5에 위치하지 않는다는 점이다. (0.9정도쯤에 위치할 가능성이 높다)
이렇게 구한 맵핑 과정은 실제로 DirectX3D에서 사용하는 방식이다.
https://learn.microsoft.com/en-us/windows/win32/dxtecharts/the-direct3d-transformation-pipeline

공식 다큐먼트를 보면 우리가 구한 식과 동일하다는 것을 알 수 있다.
코드로 살펴보자.
// Mat.h
// ...
constexpr static _Mat Projection( T w,T h,T n,T f )
{
if constexpr( S == 4 )
{
return {
(T)2.0 * n / w, (T)0.0, (T)0.0, (T)0.0,
(T)0.0, (T)2.0 * n / h, (T)0.0, (T)0.0,
(T)0.0, (T)0.0, f / (f - n), (T)1.0,
(T)0.0, (T)0.0, -n * f / (f - n), (T)0.0,
};
}
else
// ...Mat.h에 방금 구한 Projection matrix가 추가되었다.
그리고 우리가 기존 사용하던 PubeScreenTransformer를 NDCScreenTransformer로 교체할 수 있게 되었다.
로직 상 달라지는 부분은 없다.
// NDCScreenTransformer.h
#pragma once
#include "Vec3.h"
#include "Graphics.h"
class NDCScreenTransformer
{
public:
NDCScreenTransformer()
:
xFactor( float( Graphics::ScreenWidth ) / 2.0f ),
yFactor( float( Graphics::ScreenHeight ) / 2.0f )
{}
template<class Vertex>
Vertex& Transform( Vertex& v ) const
{
// perform homo -> ndc on xyz / perspective-correct interpolative divide on all other attributes
const float wInv = 1.0f / v.pos.w;
v *= wInv;
// additional divide for mapped z because it must be interpolated
// adjust position x,y from perspective normalized space
// to screen dimension space after perspective divide
v.pos.x = (v.pos.x + 1.0f) * xFactor;
v.pos.y = (-v.pos.y + 1.0f) * yFactor;
// store 1/w in w (we will need the interpolated 1/w
// so that we can recover the attributes after interp.)
v.pos.w = wInv;
return v;
}
template<class Vertex>
Vertex GetTransformed( const Vertex& v ) const
{
return Transform( Vertex( v ) );
}
private:
float xFactor;
float yFactor;
};파이프라인을 변경한다.
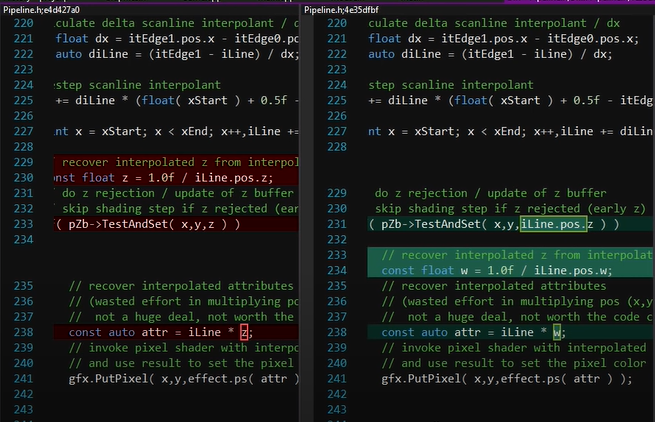
iLine.pos.z에는 z의 역수가 들어있고, w에는 z가 들어있음에 유의. (당연히 실제 3d 프레임워크에서는 이렇게 더럽게 처리되지 않을테니 이부분은 사실 크게 신경 안써도 된다)
그냥 로직 상 w에 1/z를 대입하는 중이구나, 정도만 이해해도 된다.
// prestep scanline interpolant
iLine += diLine * (float( xStart ) + 0.5f - itEdge0.pos.x);
for( int x = xStart; x < xEnd; x++,iLine += diLine )
{
// do z rejection / update of z buffer
// skip shading step if z rejected (early z)
if( pZb->TestAndSet( x,y,iLine.pos.z ) )
{
// recover interpolated z from interpolated 1/z
const float w = 1.0f / iLine.pos.w; // 해당 스코프 내에서 w를 1/z로 만들어준다
// recover interpolated attributes
// (wasted effort in multiplying pos (x,y,z) here, but
// not a huge deal, not worth the code complication to fix)
/*
여기서 Vec4의 "normalization"이 처리된다
*/
const auto attr = iLine * w;
// invoke pixel shader with interpolated vertex attributes
// and use result to set the pixel color on the screen
gfx.PutPixel( x,y,effect.ps( attr ) );
}
}
}
}
public:
Effect effect;
private:
Graphics& gfx;
NDCScreenTransformer pst;
std::shared_ptr<ZBuffer> pZb;
};SpecularPhongPointEffect를 수정해 Projection matrix가 실제로 곱해지도록 한다.

이때 주의해야 하는 점이 바로 월드좌표계에서의 TR matrix와 Projection matrix을 개별적으로 저장해야 된다는 점이다. 즉 곱 두 행렬곱 연산을 분리시켜야 한다.
이유는 projection matrix를 normal 벡터들에 곱하게 되면 normal을 변형시켜버리기 때문이다.
(TR matrix의 경우, 둘 중 Rotation만이 normal 벡터에 적용되도록 설계가 되어있다. normal 벡터는 w=0이기 때문에 translation은 무시된다. 19. Vec4, Mat4 참고)
아래 코드에서 Vertex shader 연산을 처리하는 operator() 연산자를 잘 살펴보자.
// SpecularPhongEffect.h
class VertexShader
{
// ...
public:
// 별도의 행렬 두개로 나눠 저장한다
void BindWorld( const Mat4& transformation_in )
{
world = transformation_in;
worldProj = world * proj;
}
void BindProjection( const Mat4& transformation_in )
{
proj = transformation_in;
worldProj = world * proj;
}
Output operator()( const Vertex& v ) const
{
const auto p4 = Vec4( v.pos );
return { p4 * worldProj,Vec4{ v.n,0.0f } * world,p4 * world };
/*
정점에는 projection matrix를 곱하고, 또 world matrix(TR matrix)도 곱해준다.
normal에는 world만 곱해준다.
*/
}
}SpecularPhongPointScene.h 및 몇가지 사소한 코드의 수정은 생략한다.
이렇게 새 projection matrix를 파이프라인에 적용시킨 후 실행해보면,

곧바로 무언가가 잘못되었음을 알 수 있다.
앞쪽 폴리곤이 비어보이면서 뻥 뚫려보이는 현상을 봤을 때, 우리는 Backface culling 단계에서 무언가 잘못되었다고 추측할 수 있다.

코드로 가보면 구체적인 문제 발생 원인을 알 수 있다.
우리가 Backface culling을 할 때를 생각해보면, 우리는 폴리곤 삼각형의 surface normal을 외적을 통해 구한 이후, 이 normal을 카메라에서 해당 폴리곤까지의 view vector(시선 벡터)와 내적해 둘이 이루는 각을 구하고 이 각의 크기에 따라 렌더링할지 말지를 결정했었다.
바로 여기서 문제가 발생하는 것이다.
AssembleTriangle 단계에서 정점들은 이미 전부 NDC Space 상으로 맵핑된 homogeneous coordinate인데, 이 값을 카메라 좌표와 연산해 view vector를 구하니 오류가 발생하는 것이다! (카메라 좌표는 0,0에 그대로 있으며 homogeneous coordinate가 아니기 때문)

간단히 한 줄을 추가해 고칠 수 있다. 카메라 좌표에도 Projection matrix 연산을 해주고, 그 뒤 그 좌표와 폴리곤 위치를 계산해 view vector를 구해주면 된다.
실행시켜보면, 이제 잘 작동함을 알 수 있다.

이렇게 더 나은 projection의 처리를 위해 projection matrix를 사용하도록 파이프라인을 변화시켜보았다.
이제 이렇게 변화된 파이프라인으로 우리가 당초 추가하려 했던 기능들을 추가해보자.

우선 화면 비율 조정의 경우, 아주 단순하게 SpecularPhongScene.h의 Frustum 생성 단계에서의 비율을 조정해주면 된다.

그러나 곧장 실행시키면 화면 창의 비율과 맞지 않아 찌그러짐 현상이 발생하는데, 이 역시 간단히 해결할 수 있다.

Graphics.h에서 생성되는 윈도우 창의 높이를 Frustum의 비율과 맞추어주면(640:480),

깔끔하게 동작하는 것을 볼 수 있다!
FOV 조절(커밋 a268135facf52b9888f39e7b7fa86b5368cfd7da)의 경우 약간의 수학적 연산을 사용하면 원리를 이해할 수 있다.
Projection matrix 생성 단계에서 fov값과 aspect ratio(ar;화면비율)을 입력받아 이를 통해 동적으로 projection matrix를 생성해주는 것으로, 수학적 원리는 크게 복잡하지 않다.

fov를 각으로 받아 라디안으로 변환시키고, 이 라디안 값과 aspect ratio 값을 삼각함수를 이용해 계산해 w,h를 동적으로 계산해 최종적으로 projection matrix에 적용시키는 방식이다.

FOV를 100으로 적용시켜주고 실행해주면 다음과 같다.

FOV를 높여주어도 잘 실행됨을 볼 수 있다.

마무리지으며, Opengl과의 차이점을 간략히 설명하면, OpenGl에서는 z를 0
1이 아닌 -1
1로 맵핑하기 때문에 행렬의 구조에 약간의 차이가 있다.
또 Projection matrix는 필요에 따라 수정/변경이 가능하다.
예를 들어 Orthogonal projection을 원할 경우 파이프라인을 수정하거나 할 필요 없이 그냥 projection matrix만 교체해주면 된다.

'개발 > 그래픽스' 카테고리의 다른 글
| [3DGraphics] 22. Camera view (0) | 2022.10.28 |
|---|---|
| [3DGraphics] 21. Clipping (1) | 2022.10.28 |
| [3DGraphics] 19. Implementing Vec4, Mat4 (2) | 2022.10.11 |
| [3DGraphics] 18. Specular highlights (1) | 2022.10.11 |
| [3DGraphics] 17. Phong shading & Per-pixel lighting (0) | 2022.09.09 |