어떤 행렬 A [[1 2][3 4]]가 있다.
이 행렬을 선형사상, 즉 함수로 보자.
2x2 행렬이므로 이 선형사상은 vec2를 vec2로 바꾸는 함수이다.
이 함수를 f(x)라고 해보자.
f(x1,x2) = y1, y2이다.
이를 평면 상에 나타내면 다음과 같다.

이때 이 선형사상에 의한 점의 이동을 더 쉽게 나타내기 위해
새로운 좌표축을 그려 해당 좌표축에서 이동을 나타낼 수 있다.

이렇게 같은 이동을 새 좌표축인 x'과 y'축에 대해 나타내면
이 선형사상 f(x) = Ax 은 단순히 벡터에 상수배 해주는 행위로 쉽게 나타낼 수 있다.
(x'축으로 2배 커지고, y'축으로 3배 커졌다)
이 상수를 람다로 나타내면 최종적으로 우리의 선형사상은 다음과 같이 나타낼 수 있다.
Ax = λx
이때 이 상수, 즉 람다를 고유값이라고 한다.
이번엔 이 고유값을 계산해보자.

일단 [[1 2][3 4]] [x1 x2] = λ[x1 x2]
를 정리하면 위 사진과 같은 식이 나온다. (정리하는 방법은 λ * I를 좌측의 [[1 2][3 4]]에서 빼주면 된다)
이렇게 정리한 식은 동차연립선형 방정식(Ax = 0꼴)인데, 동차연립선형 방정식은 반드시 0을 자명해로 가진다는 특성을 갖고 있다.
이때 자명해 만을 유일한 해로 가지려면 앞의 행렬(A-λI)이 역행렬이 존재해야한다는 특성이 있다.
그런데 이 경우, 위 식은 자명해 외에도 다른 해도 가져야 한다는 걸 직관적으로 알 수 있다.
만약 자명해만을 유일해로 가질 경우, 위 식은 x가 0, 즉 (0,0)벡터에 대해서만 상수배를 해준 값과 선형사상을 해준 값이 같아야 하는데, 그렇게 되면 x'과 y' 축이 생길 수가 없다. 해가 무수히 많이 있어야 점들이 모여 축을 만들기 때문이다.
때문에 (A-λI)는 역행렬이 아니어야 하고, 고로 저 식의 determinent (=행렬식, 판별식)은 0이 나와야 한다.
판별식을 전개해 2차방정식을 구해보면

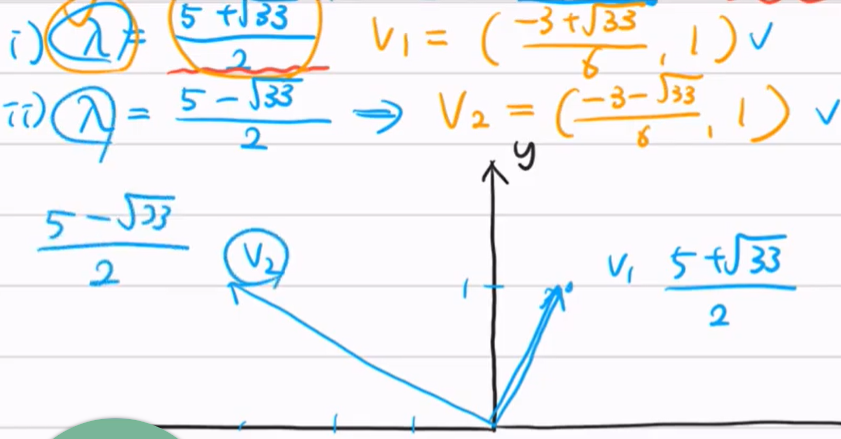
람다값이 2개가 나오는 것을 볼 수 있다. 그 중 일단 첫번째 값으로 새로 정의한 축(x', y')의 직선의 좌표를 구해보자.
람다(고유값)를 Ax = λx에 대입하면 x1, x2에 대한 식을 얻을 수 있다.

이 식이 곧 직선의 방정식이 된다. (x1를 x, x2를 y로 생각하면 우리가 흔히 생각하는 직성의 방정식 형태로 표현이 가능하다)
이 직선 위에 있는 모든 벡터들은 전부 첫번째 고유값 (5+sqrt(33))/2에 대한 고유벡터이다. e.g. ((-3+sqrt(33)) / 6, 1)
고유벡터를 해집합으로 표현하면 다음과 같다.

지금까지의 이 과정을 두번째 고유값에도 해주는 것으로 또다른 고유벡터들을(y') 구할 수 있다.
자료 출처: 수학채널 쑤튜브
https://youtu.be/FxYvAntb68s
'mathematics > linear algebra' 카테고리의 다른 글
| [선형대수] Matrix layout - Mathematics vs Graphics (0) | 2022.08.07 |
|---|---|
| [선형대수] 행렬식, 여인수전개 계산 (0) | 2022.05.19 |
